버스 대기 시간에 따른 전략

Introduction

지난 글에서 버스를 기다릴 때 length time bias가 생기는 것을 살펴보았다. 이번 글에서는 지난 번에 논한 것을 바탕으로 시뮬레이션을 해서 최적의 전략이 무엇인지 찾아보도록 하자.

이번 글에서 다루는 버스 대기 시간과 거의 유사한 문제인 지하철 대기 시간과 관련된 문제가 Think Bayes에서 Red Line problem으로 소개 되고 있다. 문제의 큰 구조는 닮아 있고 세부적인 조건이 다르니 위의 내용도 함께 참고하면 도움이 될 것이다.

TL;DR 가장 좋은 전략은 빠른 버스는 무조건 타되 느린 버스는 한 대는 무조건 보내고 다음 버스를 타는 것이다. 이렇게 하면 평균적으로 약 3분의 이익을 보게된다.

Length Time Bias의 효과

Length time bias는 여러 관측치 중 "길이"가 긴 관측치가 관측될 확률이 더 높아지는 현상을 말한다. 이런 현상은 비단 버스 대기 시간 뿐만 아니라 여성의 유방암 검출 테스트의 효능이나 간헐천의 분출 시간에도 적용된다.

유방암 검출 실험의 효능도 length time bias에 의해 체감 효능과 실제 효능이 다를 수 있다. Credit: Wikipedia

이 분포에서 어떤 값이 뽑힐 확률은 관측되는 현상의 크기에 정비례한다. 이를 확률식으로 나타내보자. PDF가 $f(x)$ 인 분포에서 위와 같은 length time bias 현상을 관측한다면 새로운 PDF는 $g(x) = \frac{xf(x)}{\mu}$ 가 된다. 이제 새롭게 정의된 PDF에서 샘플링을 해보면 length time bias의 효과를 명확하게 확인할 수 있을 것이다.

각 버스의 조건을 명시해보자. 우선 버스의 배차 간격은 정규 분포를 따른다고 가정하자. 전에도 이야기했지만 이는 엄밀하게는 틀린 가정이지만 무시하도록 하겠다. 혹시 음의 값이 샘플링 된다면 절대값을 취하거나 버리도록 하자. 애초에 음의 값이 아주 가끔 나오기 때문에 이렇게 하여도 결과에 차이를 주지는 않는다. 느린 버스인 버스 A는 평균 3, 분산 0.5를 갖는다고 하고, 빠른 버스인 버스 B는 평균 15, 분산 2를 갖는다고 하자.² 아래 실험에서 샘플링은 PyMC의 MCMC를 사용하였다.

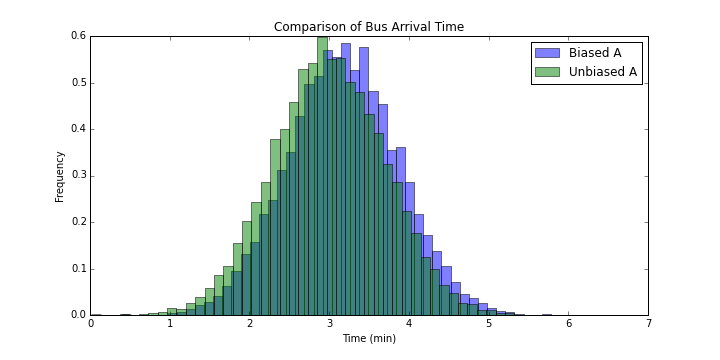
위의 차트는 평균이 3이고 분산이 0.5인 정규 분포와 length time bias가 된 정규 분포를 보여주고 있다. 여기에서 unbiased는 실제 버스 배차 간격의 분포를 의미하고, biased는 승객이 체감하는 버스 배차 간격의 분포를 뜻한다. 약간이지만 분명히 후자가 우로 편향된 경향이 있음을 알 수 있다. 보통 이렇게 히스토그램 혹은 PDF로 된 차트를 통해서 두 분포를 비교하는 것이 익숙하겠지만 이는 분포 사이의 차이를 명확하게 보기 어렵다. 더 좋은 방법은 CDF를 비교하는 것이다.¹

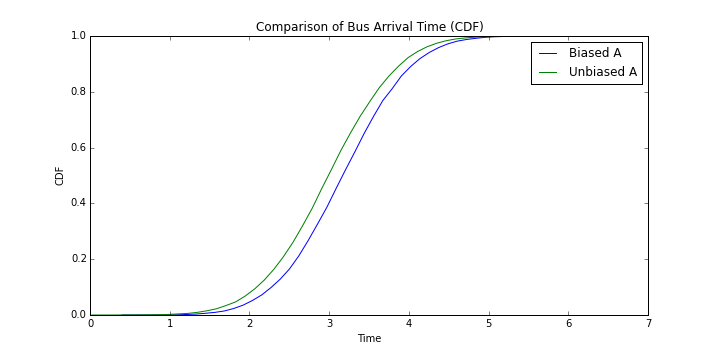
확연하게 차이가 있음을 알 수 있다.

같은 분석을 버스 B에 대해 해보자. 버스 B는 평균이 15이고 분산이 2이다.

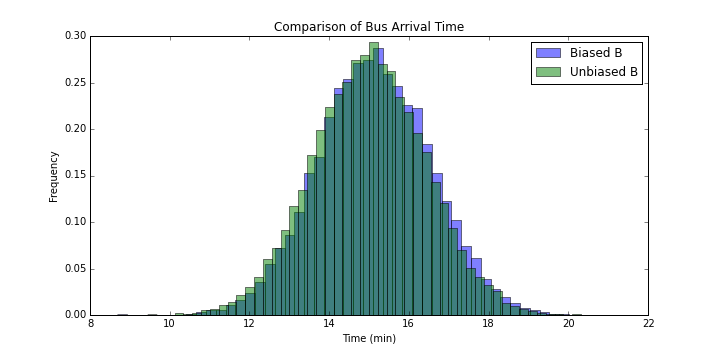
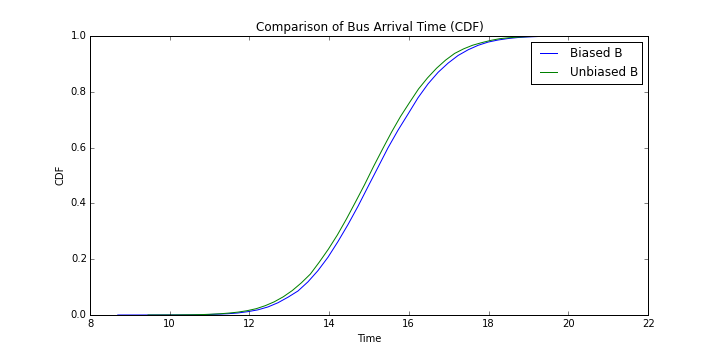
버스 A에 비하면 미묘하지만 역시 차이가 있음을 확인할 수 있다.

위의 두 예로부터 실제 배차 간격과 승객이 느끼는 배차 간격에 차이가 있음을 확실히 볼 수 있었다.

이제 승객의 입장에서 실제 대기 시간은 어떨지 생각해보자. 승객이 버스를 타러 오는 것은 푸아송 분포라고 가정해도 무방할 것이다. 즉, 어떤 시점이든 다음 승객이 도착하는 것은 항상 일정하다는 것이다. 이는 한 명의 승객 입장에서 본인이 버스를 타러 오는 시간이 대체로 일정하다면 납득할 수 있는 가정이다. 그렇다면 승객이 도착하는 것은 버스의 배차 간격 사이에 균등한 확률로 일어나게 된다. 이를 살펴보면 다음과 같다.

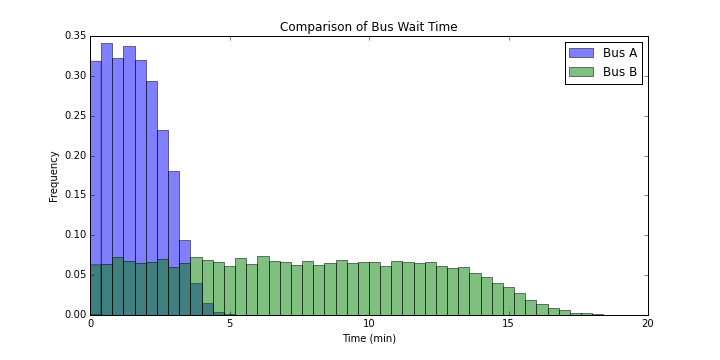
버스 A는 약 3 ~ 4분을 기점으로 확률이 줄어들고, 버스 B는 대체로 균일한 분포를 유지하다가 15분이 넘어가면 확률이 줄어드는 모습을 보인다.

전략

이제 승객이 취할 수 있는 전략을 생각해보자. 가장 생각하기 쉬운 건 먼저 오는 버스를 타는 것이다.

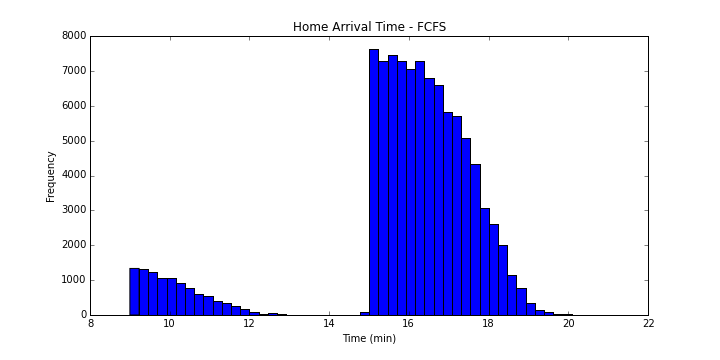
이 전략의 간략한 통계를 내보자.

• 도착 시간의 평균: 15.8322420979
• 도착 시간의 표준편차: 2.20404813293
• 도착 시간의 중앙값: 16.2538419701

약 16분 가량이 걸림을 알 수 있다.

또 다른 전략으로 이전 글에서 언급한 전략을 사용할 수도 있다.

• 버스 B가 먼저 오면 버스 B를 탄다
• 버스 A가 먼저 오면 기다린 시간에 따라 다르게 행동한다
  • 버스가 오기까지 기다린 시간이 $k$ 분이 안 되었으면 버스 A를 바로 탄다
  • $k$ 분이 지났으면 기다렸다가 버스 B를 탄다

가장 좋은 $k$ 값은 grid search를 통해 쉽게 찾을 수 있다. 아래에서는 이 전략의 최적값인 $k$ 가 3분 15초인 경우의 분석 결과를 나타낸 것이다.

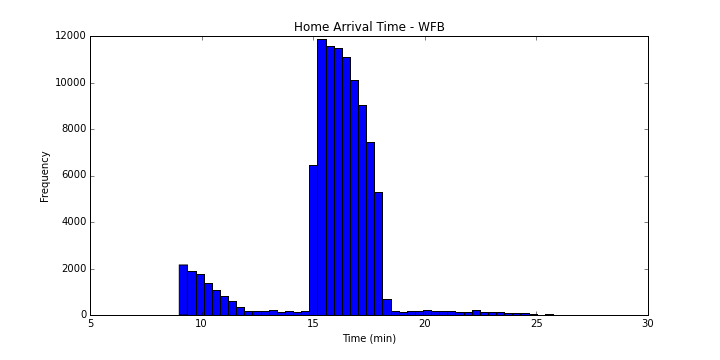
이 전략의 통계치는 다음과 같다.

• 도착 시간의 평균: 15.8198826852
• 도착 시간의 표준편차: 2.33185267677
• 도착 시간의 중앙값: 16.1961368496

기본 휴라스틱에 비해 아주 약간의 이득이 있다. 하지만 만족스러운 정도는 아니다.

조금 더 좋은 전략을 고민해보자. 방금 적용했던 전략은 구멍이 있는데, 버스 A를 한 번 보내더라도 다음에 오는 버스가 다시 버스 A일 수도 있다는 점이다. 이를 고려해서 일단 두 개의 시간 인자를 통해 첫 대기 시간과 두 번째 대기 시간을 변화 시키면서 결과를 비교해보자.

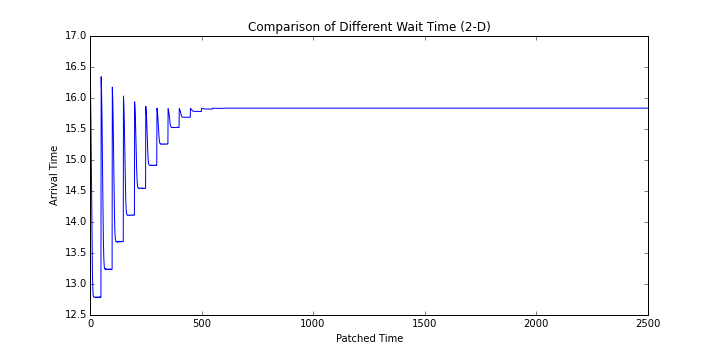
위의 차트는 살짝 보기 어렵지만 2차원 데이터를 1차원에 풀어 놓은 것이다. 코드로 표현하면 2중 루프를 도는데 외부 루프에는 첫 번째 인자를 놓고 내부 루프는 두 번째 인자를 변화 시킨 것이다. 그렇기 때문에 눈에 띄는 주기성이 생기게 된다. 의미 있는 부분만 따로 살펴보자.

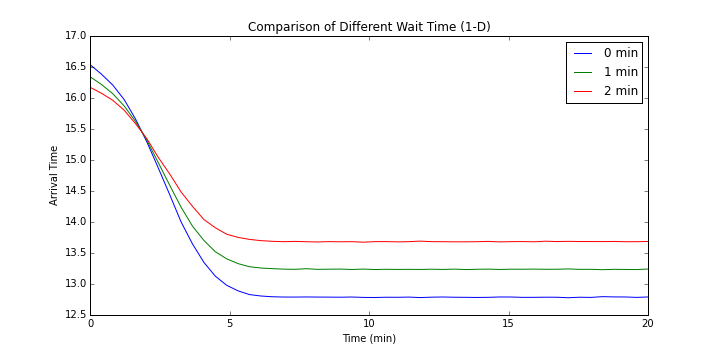
첫 번째 대기 시간은 각기 다른 선으로 나타나 있고 두 번째 대기 시간은 $x$ 축에 나타나 있다. 이를 보면 첫 번째 대기 시간은 짧은 것이 좋고 두 번째 대기 시간은 긴 것이 좋음을 알 수 있다. 위의 결과대로 전략을 짜보자.

• 버스 B가 먼저 오면 버스 B를 탄다.
• 버스 A가 먼저 온 경우 그냥 보낸다.
  • 두 번째 대기에는 먼저 온 버스를 탄다.

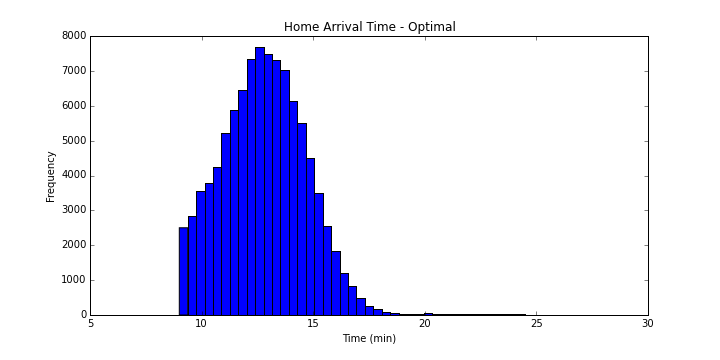
히스토그램만 봐도 이 전략이 앞의 두 전략보다 더 좋은 결과임이 자명하다. 이 전략의 통계를 내보면 다음과 같다.

• 도착 시간의 평균: 12.8397689782
• 도착 시간의 표준편차: 1.96981428863
• 도착 시간의 중앙값: 12.8200249915

앞서 논한 두 전략에 비해 약 3분 정도의 이득이 있었다.

Discussion

최종 전략을 다시 살펴보자. 이를 간단하게 말해보면 첫 버스가 B라면 그냥 타고 A라면 그냥 보낸다. 그 다음에 오는 버스는 A, B에 무관하게 무조건 타면 된다. 마지막 전략은 기본적인 휴리스틱에 비해 약 3분 가량의 득이 있다. 두 번째 버스는 무조건 타는 편이 기다리는 것에 비해 이득이기 때문에 이 전략이 아마 이 프레임에서는 최적이 아닐까 싶다.

이전 글과 이 글을 작성하는데 사용된 코드는 다음의 주소에서 찾아 볼 수 있다.

http://nbviewer.ipython.org/gist/shurain/d4b4790d011db914e608