버스 대기 시간

Introduction

얼마 전 지인 중 한 명이 다음의 문제를 페이스북에 공개하였다. 흥미로운 부분이 있기에 이를 논해보고자 한다.

학교에서 집까지 가는 방법은 버스 A를 타고 10분 동안 이동한 뒤 내려서 5분 동안 걸어가는 방법과 버스 B를 타고 8분 동안 이동한 뒤 내려서 1분 동안 걸어가는 방법이 있다. 버스 A의 배차간격은 3분이고 버스 B의 배차간격은 15분이라고 알려져 있다. (위의 상수는 임의의 숫자로 변경될 수 있음) SeoulBus나 버스정류장의 전광판 등 버스의 도착 예정 시간을 알 수 있는 방법이 없다고 할 때, 어떤 기준으로 버스를 타야 도착 시간의 기대값을 가장 빠르게 할 수 있을까?

문제가 조금은 복잡해 보이지만 정리해보면 다음과 같다.

• 버스 A: 배차 3분 이동 15분
• 버스 B: 배차 15분 이동 9분

얼핏 생각해보면 평균적으로 버스 A를 기다리는 시간은 1.5분이고 버스 B는 7.5분으로 각각 더하면 16.5분의 같은 값을 갖는 걸로 보인다. 그렇다면 나의 전략은 가장 먼저 오는 버스를 타는 것일 터이다. 과연 그럴까?

문제 설명에 주어진 것만으로는 이 문제를 풀 수 없다. 몇 가지 추가적인 가정이 필요한데, 가령 배차 간격의 분포 등이 필요하다. 그리고 그 가정에 의해 문제의 복잡도가 달라지는데 이는 length time bias 때문이다.

Length Time Bias

만약 버스가 정확하게 15분 혹은 3분의 배차 간격을 두고 운행이 된다면, 평균적으로 내가 버스를 기다리는 시간은 각각 7.5분과 1.5분이 된다. 하지만 정확하게 시간을 지키지 않고 평균적으로 그 정도의 시간만 지키면서 조금씩 달라질 수 있다면 결과가 달라지게 된다. 왜냐하면 버스 배차 간격이 긴 경우에 내가 정류장에 도달할 확률이 그렇지 않은 경우보다 높기 때문이다.

앞서 지나간 버스와 이를 뒤따르는 버스 사이의 시간 간격을 배차 간격이라 하자. 배차 간격이 주어진 경우에 승객이 정류장에 도달하는 것은 균등 분포를 따른다. 그러므로 기대 대기 시간은 배차 간격의 절반이 된다. 하지만 승객이 정류장에 도착하는 것이 균등하다면 더 큰 배차 간격에 떨어질 확률이 높다.

Credit: Mahalonobis

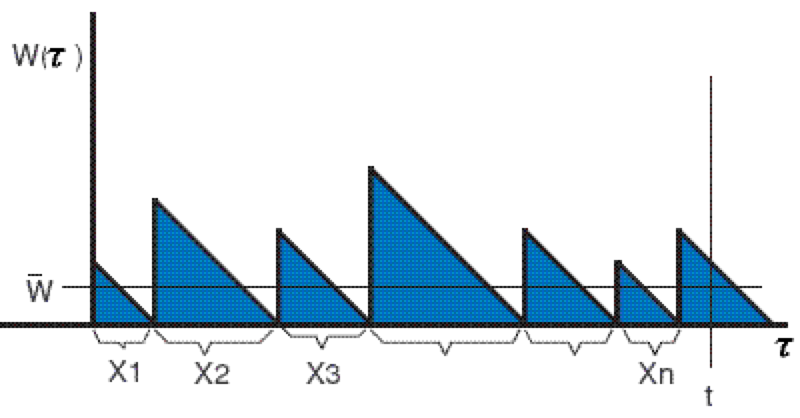
위의 이미지에서 $X_i$ 는 배차 간격, $\bar{W}$ 는 평균 대기 시간이다. 이는 위의 삼각형으로 이루어진 함수의 평균 값이 된다. $$\bar{W} = \frac{1}{t} \sum_{i=1}^n \frac{1}{2} X_i^2$$ 평균 대기 시간은 전체 시간인 $t$ 를 버스의 총 개수인 $n$ 으로 나눈 값이므로, $$\bar{W} = \frac{1}{2}\frac{\bar{X^2}}{\bar{X}}$$ 이다.

Poisson/Exponential 분포

만약 버스가 도달하는 사건이 푸아송 분포를 따른다면, 그 배차 간격은 지수 분포를 따를 것이며 다음의 수식을 만족한다.

$$Var(X) = \bar{X}^2$$

그리고 분산은 제곱의 평균 - 평균의 제곱이므로,

$$\bar{X^2} = 2\bar{X}^2$$

이를 활용하면,

$$ \bar{W} = \bar{X}$$

가 된다. 사실 이런 방법을 쓰지 않더라도 지수 분포는 memoryless 성질이 있어서 승객의 도착 시간과 무관하게 평균 대기 시간은 항상 같으므로 $\bar{W} = \bar{X}$ 임을 알 수 있다.

정규 분포

$$Var(X) = \sigma^2$$

위와 같은 방법을 사용하면,

$$\bar{X^2} = \sigma^2 + \bar{X}^2$$

이를 똑같이 대입하면,

$$\bar{W} = \frac{1}{2}\frac{\sigma^2 + \bar{X}^2}{\bar{X}}$$

이다.

만약 배차 간격이 정확하게 지켜진다면 분산은 0이 되고 그렇다면 $\bar{W} = \frac{1}{2} \bar{X}$ 가 될 것이다.

엄밀하게 말하자면 정규 분포는 음의 값을 가질 수 있으므로 배차 간격을 모델링하기에 적합하지 않다. 하지만 현실에서는 버스 사이의 배차 간격을 운전수들이 조절하려고 노력하기 때문에 (표준 편차가 현실적이라면) 배차 간격이 지수 분포를 따르지 않는 경우를 모델링 할 수 있을 것이다.

전략

버스 배차 간격이 지수 분포를 따른다면 자명하게 먼저 오는 버스를 타는 것이 가장 좋은 전략이다. 버스 B가 먼저 도착한다면 당연히 버스 B를 타는 것이 좋고, 버스 A가 먼저 도착하더라도 버스 B가 도착하기까지의 기대 대기 시간이 15분이기 때문이다.

만약 버스 배차 간격이 정규 분포를 따른다면 어떨까?

버스 B가 먼저 도착하면 당연히 버스 B를 타면 된다. 버스 A가 먼저 도착한다면 다음 버스 B가 도달하는 시간을 추론해 볼 수 있다. 내가 버스 A를 $\alpha$ 분 만큼 기다렸다면 버스 B가 도착하기까지 평균적으로 $\frac{\sigma^2 + 225}{30} - \alpha$ 분 남았다고 생각할 수 있다.¹ (분산이 충분히 작아서 무시할 수 있다고 가정하면) 남은 평균 대기 시간은 $7.5 - \alpha$ 분이다. 지금 당장 버스 A를 타면 15분 후에 집에 도착하게 되고, 버스 B를 기다렸다가 타면 평균적으로 $7.5 - \alpha +9 = 16.5 - \alpha$ 분 후에 집에 도착하게 된다. 결국 내가 1.5분 이상 버스 A를 기다렸다면, 버스 B가 오기를 기다렸다가 버스 B를 타고 내려가는 것이 평균적으로 집에 더 빠르게 도착하는 방법이 된다.

Discussion

이번 글에서는 아주 간략하게 length time bias를 소개하고 이에 따른 버스 대기 시간의 변화에 대해 논하였다. 그리고 아주 단순한 전략을 소개하였는데, 다음 글에서는 최적 전략이 무엇인지 알아보도록 하겠다.