Introduction
지난 글에 이어 Observing Dark Worlds 대회에 대한 이야기를 계속하겠다. 이번에는 1, 2위가 사용한 방법의 큰 그림을 그리면서 가능하면 자세하게 설명을 하고자 한다.
본인들이 직접 자신들의 방법을 설명한 글은 다음의 링크에서 볼 수 있다.
Decision Theory
1, 2위의 전략에 대한 설명에 앞서 decision theory에 대한 이야기를 간단하게 하도록 하겠다.
어떤 선택이 얼마나 좋은 선택이었는지 판단하기 위해서 우리는 선택의 성과를 측정할 수 있어야 한다. 보통 이런 때에는 loss function이라는 개념을 도입하여 이를 설명한다. 직관적으로, loss function은 선택의 결과와 관련된 "비용"을 나타내게 된다. 적은 비용이 드는 선택이 큰 비용이 드는 선택에 비해 좋은 것은 자명하다.
이제 우리는 선택의 성과를 측정하는 방법이 생겼으니 좋은 선택과 나쁜 선택을 구분할 수 있다. 이런 설정에서 앞으로 나아갈 자연스러운 방향은 loss의 기대값을 최소화하는 방향으로 이어지게 된다. 즉, 우리는 미리 정해진 loss function이 주어지면 expected loss를 최소화하는 어떤 선택 전략을 찾아서 이를 사용하면 된다. 그래서 실제로 expected loss를 최소화하는 문제를 푸는 시도를 하게 되는데, 이 문제를 풀다 보면 결국 posterior distribution의 계산을 해야 하는 문제에 당면하게 된다. 즉, posterior distribution의 계산이 우리의 관심사가 되게 된다.
Decision theory와 관련된 내용은 Mathematicalmonk의 decision theory 관련 동영상을 참고하기 바란다.
Bayesian Approach
전에도 언급했지만 1, 2위가 사용한 기법은 전통적인 베이지안 접근 방법이었다. 베이지안 접근 방법은 다음과 같다.
- Prior distribution을 만든다.
- Likelihood 계산을 위한 모델을 만든다.
- Bayes' theorem을 사용하여 posterior distribution을 계산한다.
- Posterior distribution에 대한 expected loss를 최소화한다.
이게 도대체 무슨 뜻인지 이야기를 해보자.
베이지안 접근 방법은 결국 세상 모든 것을 어떠한 확률식으로 표현하는 것으로 생각해볼 수 있다.[1] 우리가 보통 궁금해하는 것은, 앞 절에서도 설명하였지만, posterior distribution이다. 이는 주어진 데이터와 모델을 설명하는 모델 패러미터에 대한 식으로 나타날 수 있다.
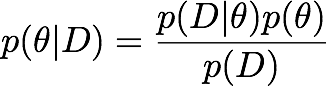
위의 수식에서 D는 우리가 관측할 수 있는 데이터이고 θ는 모델을 설명하는 모델 패러미터라고 하자. Posterior distribution은 좌변을 가리키고 likelihood는 우변의 좌측에 있는 항이며 prior distribution은 우변의 우측에 있는 항이다.
우리는 보통 어떤 데이터를 가지고 있고, 이를 토대로 모델에 대한 것을 알고 싶어 한다. 하지만 posterior distribution을 바로 계산하기는 쉽지 않다. 그렇지만 어떤 모델과 데이터가 있을 때, 그 likelihood를 계산하는 것은 상대적으로 쉬운 문제이다. 그리고 prior distribution은 결국 우리가 데이터를 관측하기 전에 각 모델이 어떤 분포를 이루고 있는지에 대한 믿음을 확률식으로 표현한 것이다. 이 두 값을 활용하여 posterior distribution을 계산하는 것이 가능하다. [2]
위의 접근 방법을 거꾸로 따라가 보자. 우리는 expected loss를 최소화하고 싶은데 이는 결국 posterior distribution을 얻는 문제로 귀결된다고 하였다. Posterior distribution을 얻는 것은 바로 위에서 설명하였다시피 likelihood와 prior distribution이 있으면 Bayes' theorem을 사용하여 계산할 수 있다. 그러므로 우리에게 필요한 것은 likelihood 계산을 위한 모델과 prior distribution이다. 이 두 확률 분포를 결정할 수 있으면 위의 방법을 순차적으로 적용하여 우리가 원하는 대로 expected loss를 최소화할 수 있다.
Bayesian Approach for Dark World
이제 실제로 대회에서 사용된 방법을 차근차근 살펴보도록 하자. 문제 자체를 생각해보면 우리가 알고 싶은 것은 각 헤일로의 위치이다. 그리고 우리가 들고 있는 데이터는 은하의 위치와 그 ellipticity 값이다. 이 두 가지를 가지고 베이지안 접근을 취해보자.
Prior Distribution
Prior distribution은 우리가 데이터를 보기 전에 각 모델에 대해 갖는 믿음의 확률 분포이다. 이 문제의 경우에는 우리가 데이터(은하의 정보)를 보기 전에 헤일로의 위치가 어떤 식으로 분포하고 있을 것인지에 대한 분포가 될 것이다. 문제의 가정에 포함되어 있었는지는 기억이 나지 않지만, 이는 자연스럽게 uniform distribution이 된다. 이는 데이터를 살펴보고 편향이 있는지 검사하여 확인할 수도 있을 것이다.
Model and Likelihood
매우 좋은 모델을 만드는 것은 사실 어려운 문제이다. 그러나 본 문제는 이미 벤치마크 코드에 어느 정도 동작하는 모델이 있었다. 주어진 모델은 완벽하지는 않지만 이를 조금만 확장하면 그럭저럭 괜찮은 모델을 만들 수 있다.
우선 가장 처음 해야 하는 것은 ellipticity에 대한 가정이다. 만약 헤일로가 없다면 각 은하의 ellipticity는 어떤 분포를 띌 것인가? 이 질문에 답할 수 있어야 모델을 만들 수 있다. 우리는 결국 각 헤일로가 은하에 미치는 영향을 ellipticity를 통해서 계산할 것이기 때문이다.
다행히도 각 은하의 ellipticity는 문제의 가정에서 특정한 편향이 없다고 주어졌다. 즉, 평범하게 평균이 0인 정규 분포를 가정하면 된다. 이 정규 분포를 설명하는 데 필요한 표준편차는 우리에게 주어진 데이터를 살펴보고 얻을 수 있다.
이제 모델을 만들어보자. 벤치마크 코드로 주어진 모델은 하나의 헤일로가 어떤 은하에 가하는 힘은 거리에 반비례하는 접선 방향의 ellipticity 계산을 통해 알 수 있다 하였다. 이는 더 정교한 모델로 바꿀 여지가 많이 있다.
우선 각 헤일로에 질량을 부여하도록 하자. 질량이 큰 헤일로가 더 큰 영향을 주는 것은 자연스러워 보인다. 은하의 질량 분포는 데이터를 살펴보아서 추측할 수 있을 것이다. 앞선 글에서도 언급하였지만, 데이터를 살펴보면 하나의 큰 헤일로와 작은 헤일로가 있으므로 이를 고려하여 질량의 분포를 예측하면 될 것이다.
그리고 데이터를 살펴보면 힘이 거리에 반비례하지만은 않는 것을 볼 수 있다. 헤일로가 은하에 가하는 힘은 단순히 거리에 반비례하기보다는 어떤 한계점이 있어서 일정 거리 이상으로 멀어지기 전에는 고정되어 있음을 알 수 있다.
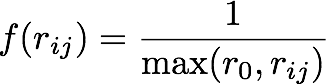
아직 더 정교화할 여지가 남아 있지만 [3] 이 정도만 하더라도 꽤 훌륭한 모델이 된다. 이를 수식으로 표현하면 다음과 같다.
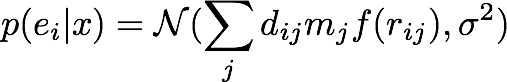
즉, 모델 (헤일로의 위치) x가 주어졌을 때, 그 모델에 의해 지금의 데이터 (은하의 ellipticity) e가 관측될 likelihood는 우리가 가정한 모델이 가하는 힘을 평균으로 갖는 정규 분포를 따른다는 것이다. 이는 바꿔 말하면 우리가 가정한 모델이 가하는 힘을 제거하고 나면 은하의 ellipticity는 평균이 0인 정규분포를 따를 것이라는 말이 된다.
여기에 더해서 2위를 차지한 사람은 헤일로의 중심에 가까워지면 노이즈가 심해져서 표준편차가 바뀔 것이라는 가정을 더하였다. 어찌 되었든 양쪽 다 모델의 모양은 거의 유사하다.
이렇게 만들어진 likelihood는 어떤 임의의 헤일로 위치와 그에 상응하는 은하의 정보가 있을 때 그런 상황이 얼마나 그럴싸한지를 표현하게 된다.
Posterior Distribution
Bayes' theorem 자체는 간단해 보이지만 실제로 posterior distribution을 계산하는 것은 어려운 문제이다. 왜냐하면 분모의 계산이 무척 어렵기 때문이다. 보통 이런 꼴의 식은 어떤 다른 패러미터에 대해 적분/덧셈을 하면 풀어낼 수 있는데, 적분 혹은 덧셈은 미천한 인간이 풀어내기 어려운 경우가 대부분이다.
비록 posterior distribution을 해석적으로 풀어낼 수는 없지만 다른 방법을 써서 이를 근사하는 것이 가능하다. 그중 한 가지 방법이 샘플링이다. 우리가 알고 싶은 분포에서 샘플을 뽑아낼 수 있으면, 그 샘플을 사용하여 원래 알고 싶었던 분포를 근사하는 것이 가능하다. 하지만 사실 이 또한 어려운 문제이다. 그러나 목표로 하는 분포의 값을 정규화하는 상수를 제외한 나머지 부분을 계산할 수 있으면 (target distribution is known up to a normalizing constant) 샘플링을 할 수 있는 Monte Carlo Markov Chain(MCMC)이라는 기법이 있다. 우리는 likelihood와 prior distribution의 값을 계산할 수 있으므로 결국 MCMC를 사용하여 원하는 대로 posterior distribution으로부터 샘플링하는 것이 가능하다.
MCMC에 대한 자세한 이야기는 나중에 다른 글에서 더 소개할 기회가 있을 것으로 여겨진다. 더 자세한 설명이 궁금하다면 Mathematicalmonk의 MCMC 설명을 참고하길 바란다.
1위는 아주 기본적인 Metropolis-Hastings 기법을 사용하였고, 2위는 그보다 더 세련된 Slice sampler를 사용하였는데 둘 다 원하는 분포에서 샘플링을 한다는 본질에는 차이가 없다. MCMC 자체가 왜 동작하는지 이해하는 것은 꽤 많은 설명이 필요하지만 그 구현 자체는 무척 간단하다.[4] 간단히 Metropolis-Hastings 기법을 이번 문제에 적용하면 다음과 같다.
Choose random halo position x[0] for i in range(1, n+1): for j in range(number of halos): Sample x by randomly moving jth halo of x[i] Calculate L(x), the likelihood of x Sample u from uniform(0, 1) if u < log L(x) - log L(x[i]): x[i+1] = x else: x[i+1] = x[i] Output x[1], ..., x[n]
알고리즘 자체는 아주 단순한 것을 알 수 있다. 놀랍게도 이렇게 출력된 x들이 우리가 원하던 posterior distribution으로부터 샘플한 값들이 된다.
Minimizing Expected Loss
Loss function은 문제로부터 주어져 있고 posterior distribution에서 뽑은 샘플도 있으므로 이제 expected loss를 구할 수 있다. 임의의 헤일로 배치 x가 주어지면 이 x의 expected loss는 각 posterior distribution에서 뽑은 샘플 하나하나를 매번 정답이라고 가정하고 구한 loss의 평균이 된다. 우리의 목표는 이를 최소화하는 x를 찾는 것이다. 이는 간단하게는 랜덤하게 많은 수의 x를 만들어보고 그 중 가장 좋은 것을 선택하는 방식을 취할 수 있을 것이다.
1위를 차지한 사람은 expected loss를 계산하면서 gradient를 계산할 수 있도록 짜서 local optimization이 가능하도록 하였다. 그리고 지역 최적점에서 빠져나올 수 있도록 random multi-start를 수행하게 하였다.
Discussion
그동안 긴 시간 공부를 하였고 소프트웨어 엔지니어로서 일도 꽤 하였는데, 그런 경험을 통해 배운 것이 하나 있다면 그건 바로 내 생각에는 구멍이 많다는 것이다. 내가 앞뒤로 모든 것을 꿰고 있는 주제가 아니라면 당연해 보이는 것들에도 늘 구멍이 있었다. 내가 프로그래머가 되어서 좋다고 생각하는 점 중 하나는 그런 구멍의 존재를 깨달을 수 있었던 부분이다. 어떤 개념/생각을 구현하는 것은 나로 하여금 생각을 아주 구체화하도록 강제한다. 논문을 읽는 동안은 전부 이해한 것 같지만 막상 구현하고자 하면 벽에 부딪히는 부분이 한둘이 아니다. 이번 대회를 통해서 실제로 베이지안 접근 방법을 적용하는 것을 보았고, 그걸 구현한 구현체도 살펴보니 많은 부분이 체화되는 것을 느낄 수 있었다. 그런 측면에서 아주 얻은 것이 많다고 할 수 있다.
[1]: 단순하게 말해서 그렇다는 것이다.
[2]: 사실 우변의 분모도 계산해야 하고 그 자체는 어려운 문제이다. 하지만 이는 데이터 D에 의해서만 결정되는 값이므로 불변이다. 그러므로 이 문제를 우회할 수 있는 방법이 있다.
[3]: 실제로는 암흑 물질의 영향을 받아서 은하의 관측 위치가 바뀌는 등 훨씬 더 복잡한 현상들이 일어난다고 한다.
[4]: 그러므로 무척 강력한 도구이다. 최초의 MCMC 기법인 Metropolis 알고리즘은 20세기 10대 알고리즘으로 선정되기도 하였다.