Introduction
수학 문제를 풀 때 유용한 전략 중 하나는 문제에 숨어있는 대칭성을 찾아서 이를 활용하는 것이다.
어떤 여행자가 강의 한쪽 편에서 맞은 편으로 가고자 한다. 밤새 심한 폭풍이 몰아쳐서 각 다리가 독립적으로 50%의 확률로 끊어졌을 수 있다. 이런 상황에서 여행자가 여전히 맞은 편으로 갈 수 있는 확률은 얼마인가?
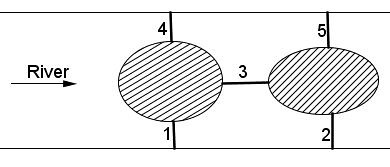
제일 먼저 떠오르는 것은 각 경우를 모두 세보는 것이다. 다리가 무너지지 않은 것을 1, 무너진 것을 0으로 표현하면 총 32가지의 경우가 있다. 이를 잘 세보면 총 16가지 경우에 다리를 건널 수 있는 것을 쉽게 확인할 수 있다. 그러므로 여행자가 강을 건널 수 있을 확률은 50%이다.
조금 다른 접근 방법으로 문제의 대칭성을 활용할 수 있다.
보트가 강을 따라서 지나가는 것을 상상해보자. 이 보트는 다리가 무너졌다면 거길 지나갈 수 있다고 가정하자. 이렇게 문제를 생각해보면 이는 위의 여행자 문제와 같은 구조를 지녔음을 알 수 있다. 다만 다리가 무너진 경우에만 지나갈 수 있는 것으로 문제가 변했을 뿐이다.
즉, 여행자가 다리를 건널 수 있는 확률과 보트가 강을 지나갈 수 있는 확률이 같다.
또한 여행자가 다리를 건널 수 있다면 보트는 지날 수 없고, 그 반대의 경우도 성립한다.
이를 바탕으로 여행자가 강을 건널 수 있는 확률은 50%임을 쉽게 확인할 수 있다.
Principle of Symmetry
위에서 본 것처럼 확률 문제에서 대칭성을 활용하여 문제에 쉽게 접근할 수 있는 경우가 종종 있다. 가장 대표적인 것이 선 위에 점이 떨어질 때의 대칭성을 활용하는 것이다.
어떤 구간에 $n$개의 점이 임의로 떨어지면, 생성되는 $n+1$개의 작은 구간은 평균적으로 같은 분포를 갖게 된다.1
이를 받아들이는 것은 약간의 상상력이 필요할 수도 있지만 여기서는 그냥 받아들이도록 하자. 이제 이런 대칭성의 법칙을 활용해서 몇 가지 문제에 적용해보자.2
The First Ace
Q: 트럼프를 섞어서 뒷면이 보이도록 순서대로 한 장씩 나열하자. 이때, 처음으로 에이스를 만날 때까지 평균적으로 몇 장의 카드를 뒤집어야 할까?
총 카드가 52장인데, 그중 에이스가 네 장이므로 이를 제외하면 총 48장의 카드가 있다. 이를 하나의 구간으로 생각하면 에이스 네 장은 이를 총 다섯 개의 구간으로 나누게 된다. 대칭성의 법칙을 적용해보면 각 구간은 평균적으로 같은 분포를 가지므로 하나의 구간은 평균적으로 $\frac{1}{5} \times 48$의 길이를 갖게 된다. 이는 9.6이고 에이스를 뒤집기 위해 한 번 더 뒤집어야 하므로 평균적으로 10.6장의 카드를 뒤집어야 한다.
The Little End of the Stick
Q: 막대기 하나를 임의의 점을 잡아서 두 토막을 낸다. 작은 조각의 평균 크기는 얼마일까?
임의의 위치를 하나 정하는 것은 막대기 위에 점이 하나 떨어지는 것으로 생각할 수 있다. 점이 떨어지는 곳은 왼쪽 절반 혹은 오른쪽 절반으로 각 위치에 떨어질 확률은 50%로 같다. 만약 왼쪽 절반에 점이 떨어졌다면, 대칭성의 법칙에 의해 점이 구간을 절반으로 나누므로 전체 막대기의 절반의 절반이 작은 조각의 크기가 된다. 오른쪽 절반도 같은 논리로 계산할 수 있다. 그러므로 평균적으로 작은 조각의 크기는 막대기 길이의 $\frac{1}{4}$이다.
German Tank Problem
Q: 주축군에서 탱크를 만들면 각각의 탱크에 일련번호를 부여한다. 이는 만들어진 순서에 따라 1부터 순서대로 매겨진다. 어느 날 연합군이 60번의 일련번호가 붙여진 탱크를 포획했다. 주축군은 총 몇 대의 탱크를 만들었을까? 연합군은 60번 탱크 한 대만 관찰하고 다른 탱크의 존재 여부는 전혀 모른다고 가정하자.
이 문제는 당연히 맞는 답이 존재하지 않는다. 하지만 여러 가지 방법으로 접근해 볼 수 있는데, 그중 하나가 대칭성의 법칙을 적용하는 것이다. 60이라는 숫자가 1 ~ N까지의 구간에 떨어진 하나의 점이라고 생각하면 이는 평균적으로 이 구간을 절반으로 나눌 것이다. 그렇다면 왼편으로 59의 작은 구간이 생기므로 오른쪽으로 59의 구간이 있을 것이라고 가정하고 총 119대의 탱크가 있다고 할 수 있다.3
Discussion
변수에 대한 사전 확률이 균등 분포를 이룬다면 위의 법칙을 활용해서 꽤 복잡한 문제에 쉽게 접근할 수 있는 것을 살펴보았다.
사실 확률의 대칭성을 고민하는 것은 위에 언급된 것보다 훨씬 심오한 의미가 있다. 위의 예제에서는 어떤 확률변수가 균등한 분포를 가짐을 가정하였지만, 이런 사전확률을 알지 못할 때에도 비슷한 가정을 하고 문제에 접근하는 전략을 예전부터 많은 수학자가 활용하였다. 이는 일견 잘 동작하지만 여러 패러독스를 만들어냈고, 이를 잘 이해하기 위한 이론적 발전이 있었다. 이와 관련된 내용은 따로 다루지는 않겠다. 관심 있는 분들은 probability와 symmetry에 대해 찾아보면 다양한 자료를 접할 수 있을 것이다.